Why he works in 96kHz 32bit Audio

[solaris]

Ok, so I saw this web page that explains why it is better to make music in 96kH. The misinformations there are just so many that it is very funny to read.
Nevertheless some people say that virtual instruments sound better (or at least different) in higher sample rates. Has anyone experienced something like this?

I know that some processes like pitch shifting or audio restoration do benefit from higher sample rates.

web page

[The Elf]

To each their own. I doubt a song ever failed to climb up the charts because the VIs weren't running at 96kHz...

[Hugh Robjohns]

The misinformations there are just so many that it is very funny to read.

Sad, rather than funny. Quite astonishing how the familiar gross misunderstandings persist, and are retold with such conviction. And he added some new ones I'd not come across before, too...

There are a few good, factually-based reasons for choosing to work at a 96kHz sample rate, and with 32 bits for general data routing and storage in the DAW in some situations. But none of those were mentioned in his article.

But at the end of the day, he can do what he likes if it makes him happy.

H

[Exalted Wombat]

The mad thing is, he isn't a purist acoustic music recordist, he's an EDM producer. 96KHz strikes as the ultimate in turd-polishing. And I'm talking about his acoustic source material, not his artistry.

[molecular]

nice picture of him recording a bass amp with a C1000s, though, so he clearly knows what he's doing... *ducks*

[oneflightup]

nice picture of him recording a bass amp with a C1000s, though, so he clearly knows what he's doing... *ducks*

+1

Nick

[Ben Asaro]

Wow, I guess all that Stuff Prism Sound was going on about at the Project Studio Expo, and all that emprical evidence, is just a pile of rubbish.

[Hugh Robjohns]

Wow, I guess all that Stuff Prism Sound was going on about at the Project Studio Expo, and all that emprical evidence, is just a pile of rubbish.

As it happens, I was originally scheduled to lecture on Prism's behalf at the PSE but was unable to attend AES this year. I don't know who was invited to give the converter lectures instead of me, but the Prism Sound guys certainly know what they are talking about...

As I said earlier, there are some perfectly valid reasons for working at 96kHz, but unfortunately I think they were all missed in that blog post, and a bunch of completely fallacious reasons invented instead... including the often-claimed 'smoother audio' and 'less pixelation' baloney!

H

[Sam Inglis]

I guess one reason for working at 96kHz if you are using virtual instruments is that it is usually possible to achieve lower latency figures, which will improve the playing experience.

[ConcertinaChap]

There are a few good, factually-based reasons for choosing to work at a 96kHz sample rate, and with 32 bits for general data routing and storage in the DAW in some situations. But none of those were mentioned in his article.

I've been doing this stuff for just long enough now to be able to see the fallacies and laugh at them too, and I'm comfortable with the sound I get working at 44.1kHz/24 bits, but I'd be interested in what the good reasons are.

Cheers,

CC

[Mixedup]

Higher sample rates give you lower latency. They make it easier for an A-D converter's filter to separate wanted signal from sidebands and thus to avoid aliasing or roll-off at the upper frequency limits of human hearing. They also give shorter pre-ringing for linear phase EQ -- though that can be achieved through oversampling in a plug-in. And they make it possible to slow down ultrasonic frequencies by playing back at a lower frequency (think wildlife etc). But there are always trade offs. And most modern converters do very well these days at 48kHz if not 44.1. And it's rare anyone's bothered about capturing 18+ kHz that accurately for most music. And sample-rate conversion (eg if converting from 96kHz recordings to mix at 44.1) can introduce its own artifacts...

That's the bits I know in a nutshell... but I'm sure there's more to say!

[ConcertinaChap]

Higher sample rates give you lower latency.

How does that work? I find that counter-intuitive since at higher sample rates you're flinging more data around which I would have thought would have worsened latency problems.

CC

[Jack Ruston]

Well, if a process incurs a delay of 96 samples, that would take 1ms at 96 kHz. At 48 kHz that same 96 sample delay would take 2ms. The 'hit' is taken by the processor which has to work harder.

J

[Hugh Robjohns]

How does that work? I find that counter-intuitive since at higher sample rates you're flinging more data around which I would have thought would have worsened latency problems.

CC

The latency here is that of the converter itself, usually around 0.75ms at 44.1kHz. Most of the latency comes from the use of an FIR filter structure which inherently involves delaying the signal for a fixed number of samples. If the sample rate is doubled, the total delay time for the same number of samples in the FIR filter is correspondingly halved.

[ConcertinaChap]

Thanks Hugh. I suspected there must be a fixed number of samples involved somewhere. Your reply also led me to look up finite impulse response filters. Well, my maths A level is an awfully long time ago now, so I didn't read too far

Cheers,

CC

[Hugh Robjohns]

The maths can get scary, but the concept isn't too hard. FIR stands for 'finite impulse response', and that describes what's going on quite well. The basic structure of an FIR filter is this:



The input data (marked as Xn above) is clocked, one sample after another, along a long string of single-sample-delays (marked here as the Z-1 boxes). So basically each sample value is stored in a memory for one sample period to allow its value to be processed, and then it's passed on to another memory store for the next sample period, and so on. The length of this notional string of memory cells is finite -- hence the FIR name. The length determines the accuracy of the filter response, to some degree, and longer is definitely better... but longer also means means more overall delay because the input signal has to move along a longer line.

The actual act of filtering relies upon the 'impulse response' part of the name.

We generally think of equalisation in terms of the frequency domain effects -- amplitude changes with frequency (and we generally ignore the partnering phase changes which relate to what's going on in the time domain).

But there is an exact equivalent of the required EQ response in the time domain, too -- amplitude changes with time -- and that's what the impulse response is all about. Just as every different kind of EQ has its own representative shape in an amplitude/frequency graph, so too is there an equivalent unique shape in the equivalent amplitude/time graph.

If you send an analogue impulse into an analogue EQ set up to apply a specific kind of filter response shape, what comes out will not be an impulse, but an extended waveform which might look something like this:



The input signal becomes 'smeared' over time, and the actual shape of the output signal is unique for the specific EQ being applied. Here are some more notional impulse responses to give a better idea of how the impulse response shape changes with different EQs:



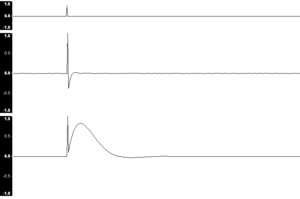
The top one is the input impulse. The middle is the impulse response after HF boost EQ, and the bottom one is after LF boost EQ.

Imagine now that we digitise those output impulse responses by sampling them at the appropriate sample rate (44.1k etc). What we then have is a system in which we input a single digital sample (the impulse), and what comes out is a long sequence of digital samples, each with a different amplitude.

That is what EQ does, and that is what the FIR filter is designed to recreate.

So going back to the diagram at the top, the input sample is passed along the storage cells, moving along a cell at each sample period. As it moves along the chain an output is taken from each step and multiplied by a coefficient (marked 'b' in the diagram) which changes the amplitude of that output sample. The multiplied sample values from every output step are summed together and passed to the FIR's output.

Remember that the multiplier coefficients are all different, and are programmed to exactly replicate the different amplitudes for each sample instant as required to create the wanted output impulse response shape (which corresponds to the desired EQ response).

So, if a single digital sample (the source impulse) is passed into this FIR chain, what comes out the end is a long stream of samples, each with different amplitudes, exactly replicating the required impulse response that defines the sound of the EQ we want.

And as each new sample in our digital audio stream follows on and enters the FIR chain, the output comprises the total combination of all of them, each being processed appropriately to generate the required equalisation effect.

In essence, we are convolving the required EQ's impulse response with the audio data stream to produce equalised audio.

Impulse responses obviously trend to zero over time, so hopefully the FIR chain is long enough that the last few multipliers would effectively always be zero. If the chain isn't long enough to achieve that for any required impulse response there will be an error in the equalisation.

The FIR approach doesn't work too well for conventional tweakable EQs because any EQ parameter change requires new multiplier coefficients at every tapping point, and that's a lot of numbers to calculate and change. So FIRs tend to be used where the required filter shape is fixed -- such as the anti-alias and reconstruction filters in converter chips!

The nature of the FIR also makes it possible to create filter impulse responses that can't exist in the analogue domain, such as linear phase filters, where the impulse response starts before the impulse actually arrives, like this:



That's easy to achieve in an FIR, because you just set the multipliers to replicate that shape along the chain, starting with very small multiplier coefficients. However, what this means is that the full height pulse representing the input impulse doesn't emerge from the output until it has progressed half-way down the line...

....and that's where most of the converter's latency comes from: waiting for the input data to reach half way down the FIR chain. For example, if the FIR chain is 68 cells long, with 34 delay cells required to generate the 'pre-ringing' part of the impulse response before the main impulse itself (and the other 34 to generate the post ringing), then the converter latency will be 34/44100 = 0.75ms (at a 44.1kHz sample rate). Longer filter chains can give more accurate and more complex filter shapes, but incur longer latencies.

As the data is clocked down the FIR chain at the sample rate, if you double the sample rate, the data travels along the chain at double speed, and hence the trip time is halved, and filter latency reduced by half as well. In the example above, that would be about 0.4ms.

In the same way, the filter's turnover frequency also maintains a fixed relationship to the sample rate, so in the case of a D-A converter's reconstruction filter, the turnover point will always be at 0.45xFs, say, and will track perfectly regardless of the chosen sample rate, which is quite neat!

(That's also why the convert chip specs define the filter turnovers in terms of the sample rate, rather than a fixed frequency.)

Hope that helps...

H

[Mixedup]

The...

You lost me at 'The'

[petev3.1]

You did better than me then.

[Hugh Robjohns]

Damn... and that was the 'LadyBird Book of Digits' version, too...

H

[Jack Ruston]

Right Robjohns, that's it. You're not coming for christmas this year.

J

[Hugh Robjohns]

[zenguitar]

A 'Classic' Robjohns explanation.

Reading through slowly and patiently, going back and reading bits again, and suddenly I really do understand. It makes perfect sense. If asked, I could even explain it myself.

Ten minutes later, I haven't a clue again. Although subsequent rereading will get the broad principles hammered home. I call it the 'Robjohns Effect'.

Hugh has a talent for explaining technical things in a way that makes them look simple. You only realise how complicated they are when you try to think it through for yourself later. But I do learn

Hugh Robjohns - Helpfully confusing the masses for 2 decades and still counting.

Andy

[AdiT]

Interesting subject, about it I will make two mentions:
- when make sense and when not link;
- there is a theory in which the phase is shifted depending of freq link .

I made some tests on my NI KA 6 at different sample rate. The output sample was at 44.1kHz and 48kHz, limited by REW.

[Hugh Robjohns]

Hugh Robjohns - Helpfully confusing the masses for 2 decades and still counting.

I'm going to get that line added to my business cards!

H

[damoore]

But don't you need twice the stages in the filter when you double the sample rate to get the same filtering effect - otherwise surely you just doubled (or whatever) the centre frequency of the filter.

Which for sampling, happens to be what you want, assuming you are doubling the cutoff frequency, but for a general filter, that isn't the case.